Performance of a LED flat plate heat sink in multiple orientations

Heat sinks are used to cool light emitting diodes (LEDs) in a similar manner to many other semi-conductor devices such as MOSFETs, CPUs and simple diodes. However LEDs because of their varied applications can be installed in various orientations unlike other semi-conductor devices which typically have a fixed orientation. The heat sinks to which LEDs are attached must be able to maintain the LED junction temperature below the specified limits in any of these orientations. If a sheet of aluminum or copper is used as the LED heat sink the thermal performance of this sheet will change depending on its orientation.

Figure 1. LED flat plate heat sink

In the blog article How to design a flat plate heat sink the analysis of a vertical flat plate heat sink cooled via natural convection and radiation is explained. In this article we’ll explain the heat sink thermal resistance calculations necessary to estimate the thermal performance of a flat plate heat sinks in the two additional orientations as shown in figure 1. Analyses for a flat plate heat sink oriented at incremental angles between the vertical orientation, horizontal orientation with the heated surface facing up and the horizontal orientation with the heated surfacing down will not be provided since the thermal performance will lie some where between these three orientations. The horizontal orientation with hot surface facing down typically has the worst performance.

The orientation of the flat plate heat sink has no effect on conduction from the LED heat source through the flat plate to the external surface and radiation from the external surface. Please refer to the blog article How to design a flat plate heat sink for a detailed explanation of the junction to case resistance, contact/thermal interface resistance and radiation resistance calculations for a flat plate heat sink.

The equation for thermal convection resistance R_conv from the surface of a horizontal flat plate with the heated surface facing upward or downward is given by equation 6. The corresponding average Nusselt number, Nu_L for each orientation (equations 1 and 2), [1] are used to calculate the convection thermal resistance R_conv of each orientation. Using the procedure and equations described in the blog post How to design a flat plate heat sink and replacing the thermal convection resistance equation with equation 6 the performance of the flat plate LED heat sink can be estimated.

horizontal flat plate with the heated surface facing upward
$\displaystyle \overline{Nu}_{L}=\left [\left (0.54Ra{_{L}}^{1/4} \right )^{-4}+\left (0.15Ra{_{L}}^{1/3} \right )^{-4} \right ]^{-1/4}$ 1

horizontal flat plate with the heated surface facing downward
$\displaystyle \overline{Nu}_{L}=0.52Ra{_{L}}^{1/5}$ 2

where:

$\displaystyle Ra_{L}=\frac{g\beta (T_{s}-T_{amb}){\widehat{L}}^{3}}{\nu \alpha }$ 3

$\displaystyle \widehat{L}=\frac{LW}{2\left (L+W \right )}$ 4

$\displaystyle T_{s}$ is the surface temperature of the plate

$\displaystyle T_{amb}$ is the ambient air temperature

$\displaystyle g$ acceleration due to gravity

$\displaystyle T_{avg}=(T_{s}+T_{amb})/2$ 5

$\displaystyle \nu$ is the kinematic viscosity of air evaluated at T_avg

$\displaystyle \alpha$ is the thermal diffusivity of air evaluated at T_avg

$\displaystyle \overline{h}=\overline{Nu}_{L}\times k_{air}/L$ 6

where:

$\displaystyle k_{air}$ is the thermal conductivity of air evaluated at T_avg

$\displaystyle R_{conv}=\frac{1}{\overline{h}A_{p}}$ 7

Accounting for multiple LEDs
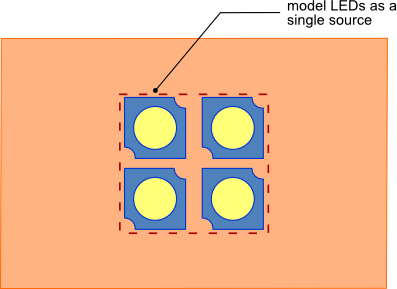
If multiple identical LEDs are being cooled by the heat sink and they are spaced very close to one another then a reasonable approximation is to assume that the LEDs are equivalent to one single large heat source as shown if figure 2. The heat source should have an area that is equivalent to the sum of the areas of the LEDs that are in contact with the heat sink. The equivalent interface (R_int-eqv) and junction to case thermal (R_th-jc-eqv) resistances for the single equivalent heat source need to be calculated as shown in equations 8 and 9.

Figure 2. Multiple closely spaced LEDs modeled as a single LED

$\displaystyle R_{int-eqv}=\frac{R_{int-single}}{N}$ 8

$\displaystyle R_{th-jc-eqv}=\frac{R_{th-jc-single}}{N}$ 9

where:

$\displaystyle R_{int-single}$ is the thermal interface resistance of single LED

$\displaystyle R_{th-jc-single}$ is the junction to case thermal resistance of single LED

$\displaystyle N$ is the number of LEDs

An online heat sink calculator based on the calculation methodology described in this blog post is available free of cost. Click the following link to access the calculator: Flat Plate Heat Sink Calculator

[1] F. Incropera, D. DeWitt, (2011). Fundamentals of Heat and Mass Transfer (7th ed.). Hoboken: Wiley. pp. 610